Text Clustering with tf-idf
Table of Contents
Background
Edited from a Smart Learning Report (SLR) written at Procter & Gamble R&D (co-authored with Alex Gutman). This is the supporting theory for the analysis of consumer comments and an associated R Shiny App that helped detect copycat consumer complaints using text similarity. Copycat complaints are highly associated with fraud attempts to collect financial compensation on the basis of alleged product failure (specially in the US).
Summary
Large organizations often deal with high volumes of text corpora , this often creates the need to group documents according to some concept of similarity. If done manually, this can be a slow and painful process, not to mention prone to human error and difficult to scale. In this SLR we describe an automated NLP approach to cluster documents based on term frequency–inverse document frequency (tf–idf) and cosine similarity .
Problem Statement
Our initial input is a set of documents in English—in the form of consumer comments—that we would like to group together such that documents belonging to the same cluster are similar and documents belonging to different clusters are dissimilar.
Preliminaries
Basic Information Retrieval Terminology
In linguistics a word is considered to be the smallest meaningful element that can be uttered. Words are usually referred to as terms (to account for other word-like objects like numbers). A group of terms forms a document; a document could be the chapter of a book, a tweet, or a consumer comment. A collection of documents constitutes a corpus. Once the corpus is recreated as a data structure on the computer, then users can run Information Retrieval (IR) queries against it.
Term-Document Matrix
The process of storing and representing a corpus efficiently in a computer for future information extraction is a central theme in IR. A common approach is via indexing. This is done by taking each document and each term in the corpus and building a matrix with documents as columns and terms as rows—this is the so-called term-document matrix (tdm) (or inversely, a document-term matrix).
The cells of this matrix are filled by values that connect the terms and the documents according to some function. The trivial representation would be the (binary) incidence matrix—in which each (document, term) cell value is 1 if the term is present in the document, 0 otherwise. Another common approach is to use raw frequency counts. In this SLR we use tf-idf, a slightly more sophisticated method.
Solution Design
The first step should be to come up with a mathematical representation of the corpus amenable to further modeling. Then, from the problem statement, it follows that we need to define a quantitative measure of similarity that will allow us to calculate a similarity score between any two documents in the corpus. Finally, we will feed these scores to some clustering algorithm to end up with document clusters. Documents within the same cluster are candidates for copycat complaints.
In short, the overall solution encompasses the sequential solution of three sub-problems1: i) corpus representation, ii) similarity score and iii) clustering algorithm.
Corpus Representation : tf-idf
Tf–idf has two components:
-
term frequencies (tf): term frequencies are the frequency counts of each term in each document. The frequency of term \(i \) in document \(j \) will be denoted by \(tf_{i,j} \)
-
inverse document frequency (idf): idf is defined as \( log(N/n_{i}) \); where \(N\) is the number of documents in the corpus and \( n_{i}\) is the number of documents that contain term \(i \). The purpose of the logarithm is to decrease the size bias in corpora with large amounts of documents.
The intuition behind term frequencies is simple: the more a term appears in a document, the higher its importance and therefore its weight. But words are not equally important in significance, some words are so frequent that their predictive value is negligible, and/or they have no intrinsic meaning—such is the case with the so-called “stop words” (e.g. in English: “to”, “for”, “in”, etc)2.
At the other end of the spectrum, some terms are rare and meaningful. The extreme case is called hapax legomenon (i.e. a word that appears only once in a given corpus). We would expect documents that share rare and meaningful words to be somewhat related to each other. This effect is modeled mathematically using idf3.
Therefore, multiplying (1) and (2) we obtain a weight function that combines the term’s document frequency with a balancing factor that accounts for the term’s rarity in the corpus. The final function is as follows4:
\[ w_{i.j} = tf_{i,j} \times log(N/n_{i}) \hspace{1.5cm} (1) \]
The tdm with tf-idf weights then becomes our input for the similarity score sub-problem.
Similarity Score : Cosine Similarity
For practical reasons we will follow a bag-of-words approach: the terms contained in each document become its features—or dimensions—and word order is immaterial. This is a convenient way to model the tdm in the vector space. In which each document is represented by a vector of tf–idf weights.
All vectors share the same cardinality. However, the majority of elements of any given vector will have a value of 0, as it is expected that any given document uses only a fraction of all of the unique terms found in the corpus.
Visually, the \( n \) total distinct terms of the corpus create an \( n \)-dimensional space—in which the (feature) values of each vector represent the “position” of the document in those dimensions. This representation allows us to compute the cosine of any two vectors in the vector space and find out how “close” they are.
It is important to note that the cosine is not a measure of magnitude—but rather of orientation—between two vectors. The cosine of two maximally similar (i.e. parallel) vectors is 1, whereas the cosine of two maximally dissimilar (i.e. orthogonal) vectors is 0.
The formula for cosine similarity can be interpreted as the normalized dot product of two vectors. Or more explicitly, as the dot product of two vectors divided by the product of their (squared-then-rooted) dimensional lengths:
\[ Cosine (X, Y) = \frac{ \Sigma^{n}_{i=1}{x_i \times y_i} } { \sqrt{ \Sigma_1^n{x^2_i }} \times \sqrt{ \Sigma_1^n{y^2_i }} } \hspace{1.5cm} (2) \]
After applying (2) to all unique document pairs in the corpus, we will end up with a cosine similarity matrix, our input for the clustering sub-problem.
Clustering Algorithm : Hierarchical Clustering
We now have a similarity matrix that assigns a value from 0 to 1 to any two documents in the corpus. With 1 being most similar and 0 being most dissimilar. There are many types of clustering methods, each with pros and cons depending on the type of problem at hand. We will follow a Hierarchical Clustering (HC) approach.
Hierarchical clustering operates on a notion of distance as opposed to similarity, so we will take the complement of the cosine (i.e. a similarity of 1 becomes a distance of 0). This will result in similar documents being placed closer together and therefore being clustered earlier in the process.
One of the most appealing features of HC is that the user does not need to predefine the number of clusters. One drawback, is that he still needs to decide where to cut the final tree or dendrogram—and this choice has direct impact on the number of resulting clusters.
The iterative HC algorithm is as follows5:
- Begin with \( n \) observations and a measure (such as Euclidean distance) of all the \( {n\choose 2} = n(n − 1)/2 \) pairwise dissimilarities. Treat each observation as its own cluster.
- For \( i = n, n − 1, . . . , 2 \):
(a) Examine all pairwise inter-cluster dissimilarities among the \( i \) clusters and identify the pair of clusters that are least dissimilar (that is, most similar). Fuse these two clusters. The dissimilarity between these two clusters indicates the height in the dendrogram at which the fusion should be placed.
(b) Compute the new pairwise inter-cluster dissimilarities among the \( i − 1 \) remaining clusters.
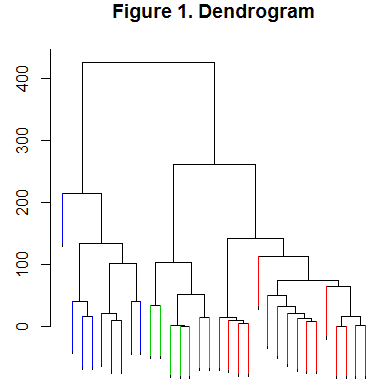
Dendrogram
Finally, we can cut the tree at some height to produce the final clusters. Figure 1 displays an example dendrogram cut at a height of 250, resulting in 3 distinct clusters: blue, green and red.
Appendix
Natural Language Processing
Natural Language Processing (NLP) is a field of computing concerned with the interactions between human (i.e. natural) languages and computers. It is not a straightforward task to process natural languages in a computer. There are many aspects in language that provide structure and meaning that computers struggle with: intonation, emotion, punctuation and word order are some of the most important. Creating a data structure that accurately captures all the multidimensional nuances in text and speech remains one of the most challenging areas in computing.
Information Retrieval
Information Retrieval (IR) is a field of computing that deals with finding information (usually documents or parts of documents) in large collections of data, based on specific query needs. IR is found in and around related applications such as classification (where the objective is to assign documents to a given a set of classes), and clustering (where the objective is to group documents based on their contents). This SLR is about document clustering.
Notes
-
Each of these sub-problems is a problem in its own right, sometimes with multiple competing solutions. Further, the approach used to solve one sub-problem can significantly affect the overall results. Therefore it is advised to try different approaches and contrast them. ↩︎
-
See the following toy examples using a corpus of size \(N = 100 \). Case 1: if term \(i \) is found in every document in the corpus, then \( N/n_{i} \) will evaluate to 1 (i.e. smaller weight factor). Case 2: if term \(i \) is found in only one document in the corpus, then it will evaluate to 100 (i.e. larger weight factor). The intuition behind idf is to provide a factor that increases with term rarity in a “restrained” fashion—ergo the logarithm encapsulation. ↩︎
-
Taken from the classic An Introduction to Statistical Learning with Applications in R . Tibshirani et al (2013). Chapter 10: Unsupervised Learning. There are two choices the analyst will have to make before running the algorithm: i) the dissimilarity measure, and ii) the linkage method. ISLA provides a good overview of the available alternatives and their trade-offs. ↩︎