Elements of Hyperdimensional Cubes
Table of Contents
Summary
A review of the building blocks of lower-dimensional cubes and the functions that describe their transformations into higher dimensions. We’ll begin by working with points, segments, squares, and cubes. By observing these lower-level objects we’ll be able to derive generalized formulas valid for the n-cube. These equations will describe precisely all constituent elements of any hypercube.
Introduction
One way of describing the processes involved in going from lower to higher dimensions is through motion. When a point moves to another point, this movement traces out a segment in a new dimension. In turn, a segment sweeps out to create a square, a square a cube, a cube a tesseract (Figure 1), etc. It can go on indefinitely.
Figure 1. Point, segment, square, cube and tesseract1
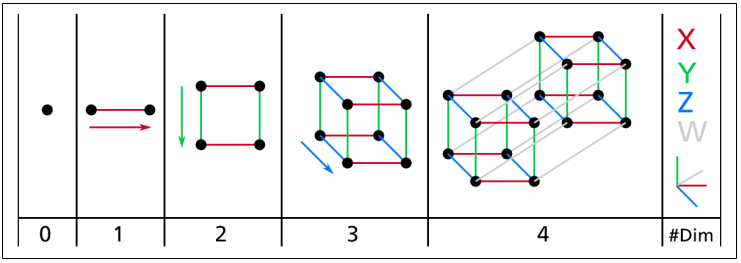
Note that although the cube2 is tacitly understood as the 3-cube, I will also be making use of standard n-cube notation for all dimensions, both lower and higher. Thus an edge becomes a 1-cube, and a penteract a 5-cube. This is a covenient standardization scheme, specially considering that individualized names can become a bit unwieldy for more complex figures (see Table 1).
Table 1. Nomenclature—Zero to Six-Dimensional Cubes
| Dim | n-cube | Names |
|---|---|---|
| 0D | 0-cube | Point, Vertex |
| 1D | 1-cube | Segment, Edge, -gon |
| 2D | 2-cube | Square, Face, Tetragon |
| 3D | 3-cube | Cube, Cell, Hexahedron |
| 4D | 4-cube | Tesseract, 8-Cell, Tetracube, Octachoron |
| 5D | 5-cube | Penteract, Deca-5-tope, Decateron |
| 6D | 6-cube | Hexeract, Dodeca-6-tope, Dodecapeton |
The Building Blocks—Vertices & Edges
Let’s define some foundational concepts.
- Point—the lowest level of abstraction in geometry, it represents location, with no extent3.
- Vertex—a point where two or more edges meet; they are [at] the corners of a hypercube. All vertices are points, but not all points are vertices.
- Edge—a segment connecting 2 vertices.
- \( V \)—the set of all vertices.
- \( E \)—the set of all edges.
As dimensionality \( (n) \) grows, \( V \) and \( E \) also grow, thereby reshaping the hypercube. Our goal is to understand and describe this transformation mathematically for all dimensions. Fortunately for us, these mechanics can be formulated explicitly at lower dimensions and then extrapolated into higher dimensions.
First, let’s look at vertices. To move to dimension \( n + 1 \) from dimension \( n \), the number of vertices doubles. Segments have 2 vertices, squares have 4, cubes have 8, and so on. That is to say, vertices grow at a rate of \( 2^n \). Consequently, each dimension has twice the number of vertices as its predecessor, \( |V|_{n} = 2|V|_{n-1} \).
Then we have edges. Edges can be thought of as the traces left behind by the shifting of vertices into a higher dimension (Figure 2). In other words, the vertices of dimension \( n \) travel to dimension \( n + 1 \), building a new set of edges in the process. Let’s find out how many exactly.
Figure 2. A Point Sweeps out into 3D Space4
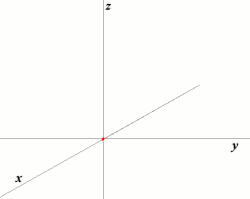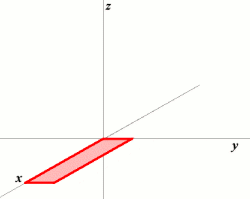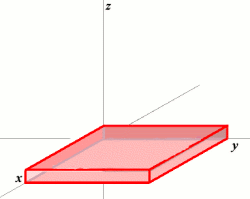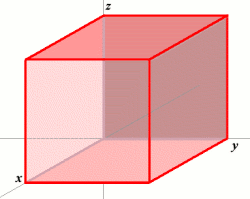
The simplest way to derive the edge count in dimension \( n \) is probably by observing the following invariant: the number of edges in \( n \) is always \( n \), times the number of vertices in the previous dimension (which we already generalized)—that is, \( n \times 2^{n-1} \). Thus, 2-cubes have \( 2 \times 2^{1} = 4 \) edges, 3-cubes have \( 3 \times 2^{2} = 12 \) edges, and so on. Note how this formula depends exclusively on \( n \), unlike other methods5.
Table 2. Vertices and Edges for an N-cube
| \( n \) | Vertices | Edges | Squares |
|---|---|---|---|
| 0 (Point) | 1 | 0 | 0 |
| 1 (Edge) | 2 | 1 | 0 |
| 2 (Square) | 4 | 4 | 1 |
| 3 (Cube) | 8 | 12 | ? |
| … | … | … | … |
| n-cube | \( 2^n \) | \( n \times 2^{n-1} \) | ? |
We are now able to determine mechanically the vertex and edge counts of any n-cube (Table 2). That completes our understanding of the elements of the square, but there are still missing elements in all higher-dimensional cubes, \( n \ge 3 \). For example, we know that a cube also has square faces, and we have no formula for the counting of squares.
In general, any \( n \)-cube is built by composing all its lower-level \( (n-k) \)-cubes, with \( k \in \{ 1, …, n \} \). It follows, by example, that a full accounting of the 7-cube requires knowing how many [0-6]-cubes it contains. But this structure seems a bit daunting to conceive, hence our next task is to devise a general formula that yields the precise count of k-cubes in an n-cube directly.
Generalizing to N Dimensions
By now we have repeated the shifting procedure a few times, and some patterns have begun to emerge. Namely, the way to construct the next dimensional cube is always by duplicating the cube in the current dimension and moving it perpendicularly to itself6. Due to the reflective nature of this procedure, the resulting higher-dimensional cubes are inherently and increasingly symmetric.
(…) grouping the faces of an object is particularly effective when the object possesses a great deal of symmetry, as does the hypercube. A segment possesses one symmetry, obtained by interchanging its endpoints. A square has a much larger number of symmetries: we can rotate the square into itself by one, two, or three quarter-turns about its center, and we can reflect the square across either of its diagonals, or across the horizontal or vertical lines through its center. The even larger group of symmetries of the cube enables us to move any vertex to any other vertex (…) The collection of symmetries is one of the most important examples of an algebraic structure known as a group .
—Banchoff7
The key observation to obtain a general formulation begins with the vertex. All vertices of an n-cube are constructed identically, therefore an entire n-cube can be generated by looking at a single n-vertex.
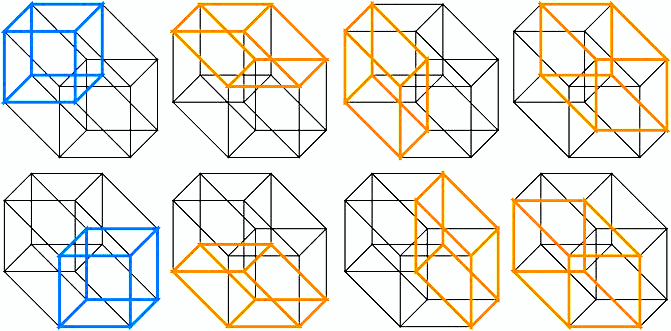
For instance, in a tesseract each vertex projects 4 edges—which means that at each vertex there are as many 3-cubes as ways of choosing subsets of 3 edges out of 4. Mathematically, this is expressed by the binomial coefficient , \( nCk = 4C3 = 4 \) ways per vertex. Multiplied by 16 vertices in the tesseract for a total of 64. But each cube uses only 8 vertices, so we divide 64 by 8 to arrive at the fact that a tesseract contains 8 cubes (Figure 3).
Figure 3. A 2D Representation of a Tesseract’s Eight 3D-Cubes8
Let’s generalize. In dimension \( n \) each vertex projects \( n \) edges. At each vertex we can determine in how many ways we can choose bundles of \( k \) out of these \( n \) edges (\( nCk \)). Then, in order to create k-dimensional cubes, this coefficient is multiplied by the number of vertices in the \( n \)-cube \( (2^n) \) and divided by the number of vertices in the \( k \)-cube \( (2^k) \); thereby obtaining the quantity of k-cubes contained in an n-cube \( (Q) \). After subtracting the powers we get:
\[ Q(k, n) = nCk \times 2^{(n-k)} \hspace{1cm} (1) \]
Turns out, (1) is the only equation we will need to take full inventory of all elements of a hypercube. In Table 3, we used it to crunch the numbers up to the 9-cube. The formulas we derived before, for vertices and edges, are actually two special cases of (1)9. Note also two intuitive notions confirmed by the table: a) any n-cube is self-contained (diagonal of ones); b) any n-cube contains zero \( (n + k) \)-cubes, for \( k > 0 \).
Table 3. Statistics of All Elements in 0-9D Cubes
| k=0 | k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | k=7 | k=8 | k=9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| n=0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| n=1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| n=2 | 4 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| n=3 | 8 | 12 | 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| n=4 | 16 | 32 | 24 | 8 | 1 | 0 | 0 | 0 | 0 | 0 |
| n=5 | 32 | 80 | 80 | 40 | 10 | 1 | 0 | 0 | 0 | 0 |
| n=6 | 64 | 192 | 240 | 160 | 60 | 12 | 1 | 0 | 0 | 0 |
| n=7 | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | 0 | 0 |
| n=8 | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 | 0 |
| n=9 | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 1 |
The N-Cube In Code
The code below implements the N_cube class in Python. The method named all_elements_matrix was used to generate the contents of Table 3.
import numpy as np
from math import comb
class N_cube:
"""Compute the counts of all lower-dimensional elements of an n-cube"""
def kcubes_in_ncube(self, k=2, n=3):
"""Return the number of k-cubes in an n-cube."""
k, n = int(k), int(n)
k_cubes = 2 ** (n - k) * comb(n, k)
return int(k_cubes)
def all_elements_matrix(self, n=5):
"""Compute the counts of all (n-k)-cubes"""
ks, ns = np.arange(n), np.arange(n)
n_statistics = [self.kcubes_in_ncube(k, n) for k in ks for n in ns]
n_statistics = np.array(n_statistics)
n_statistics = n_statistics.reshape(n, n, order="F")
return n_statistics
def elements(self, n):
"""Return element counts for a single n-cube"""
elements = self.all_elements_matrix(n + 1)
n_cube_elements = elements[n]
return n_cube_elements
# instantiate and call
n_cube = N_cube()
n_cube.kcubes_in_ncube(k=2, n=3) # 6 squares in a cube
n_cube.all_elements_matrix(10) # see Table 3
n_cube.elements(3) # array([ 8, 12, 6, 1])
Notes
-
Wikipedia – Tesseract . By user Nerd‐Boy1392 (Creative Commons BY-SA 3.0) ↩︎
-
From French cube (13c.) and directly from Latin cubus, from Greek kybos “a six-sided die,” used metaphorically of dice-like blocks of any sort (…) – Etymology.com ↩︎
-
Physics Insights.org – Hypercubes ↩︎
-
For example, here’s another way to derive the edge count that depends on more than \( n \): we know that as we shift into the next dimension, \( n + 1 \), \( |V| \) exactly doubles; necessarily, \( |E| \) also doubles. So now we have a lower bound of \( 2|E|_{n} \) and we still need to add the new edges—the traces that connect these two dimensions. This number is identical to the number of vertices they need to connect, i.e. \( |V|_{n} \). Therefore, the total number of edges \( |E|_{n+1} \), could also be determined by the formula: \( 2|E|_{n} + |V|_{n} \). However, this formula is recursive on \( |E| \) which makes it less convenient if the number of edges in \( n \) is unknown. ↩︎
-
For instance, from 2D to 3D, after the square is duplicated we have 2 squares, plus the 4 squares outlined by the shifting of the copy, for a total of 6 squares (this is why the cube is also called hexa-hedron, or “six faces”). ↩︎
-
Banchoff – Beyond3D – Counting the Faces of Higher-Dimensional Cubes ↩︎
-
Instructable Workshop – Tesseract Model .—Color scheme my own. ↩︎
-
For vertices, \( 2^{(n-k)} \times nCk = 2^{(n-0)} \times nC0 = 2^n \times 1 = 2^n\) and. For edges, \( 2^{(n-1)} \times nC1 = 2^{(n-1)} \times n \). ↩︎