Monty Hall Simulation & Law of Large Numbers

June 2018

Summary

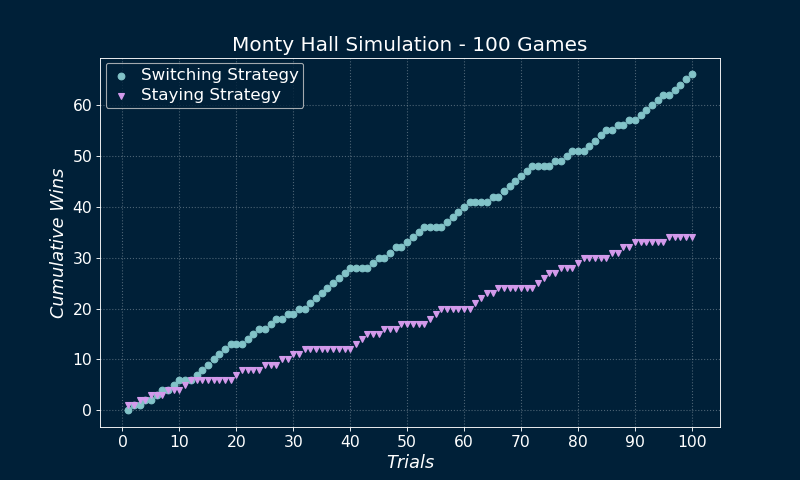
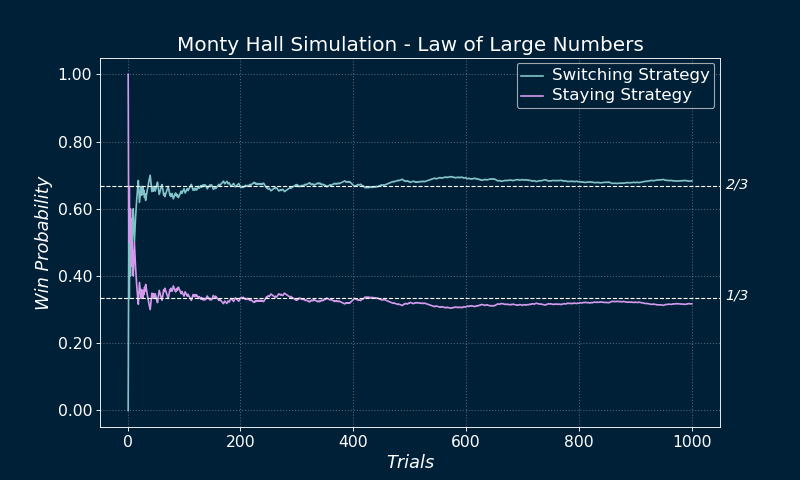
The Monty Hall Problem is a classic problem in Probability, it’s also an interesting piece of history connecting television, mathematics, programming and decision making. There are different ways to solve it and also different problem formulations. I’ll begin with the original formulation and then solve it via simulation in Python. The idea is to play the game thousands of times, analyze the results, and then use them to illustrate the Law of Large Numbers .

Problem Statement

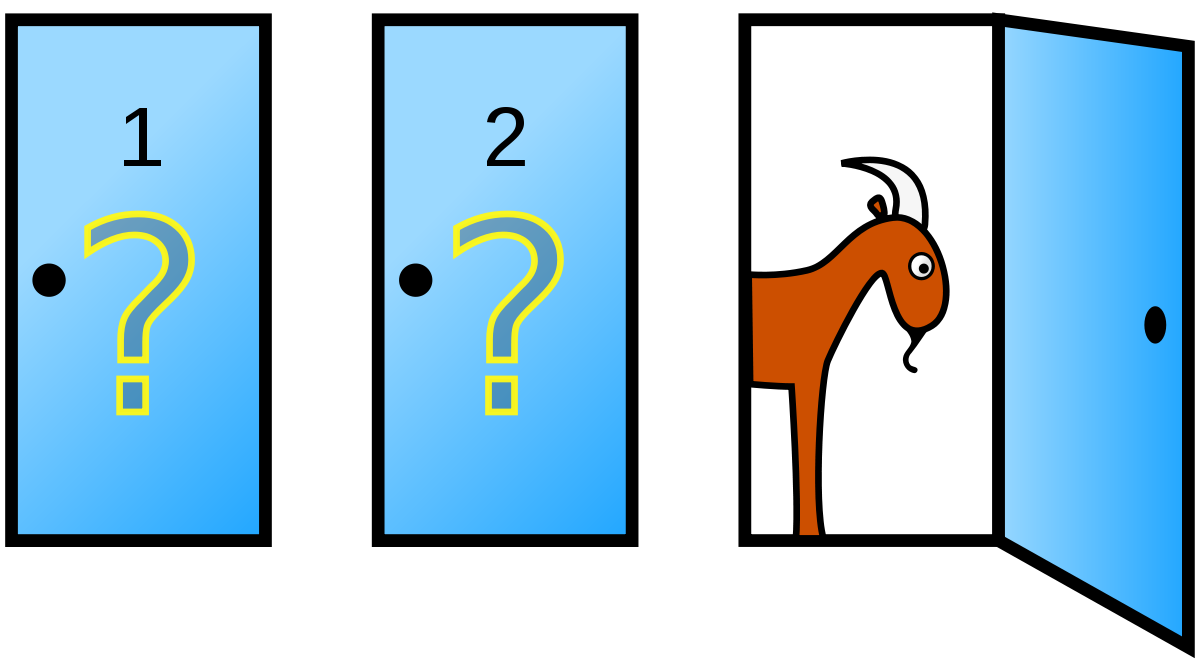
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?

Key Insights

Some people choose not to switch doors on the basis that switching or staying would make no difference. That is, the host opening the door has no effect at all on the game’s win/lose probabilities. But that is not true because as the host chooses which door to open, he creates a new experiment and draws from a different set, with different w/l probabilities.

Let’s go through a game in steps. The game begins and the player chooses a door. In turn, the host must open another door, but he has 2 restrictions: he can’t pick the player’s choice nor the winning choice. Then, we note that depending on the player’s choice, these two doors could actually coincide (i.e. the player’s choice is the winning choice). If they do coincide, then the host could open any of the two remaining doors indistinctly, since they are both false. If they don’t coincide, then he must choose the remaining false door over the winning choice.

Probabilities

Let’s assume the initial experiment of assigning a prize to a door is described using a uniform distribution . Then at the start of the game, each door has probability 1/3 of having the prize. That is, the player’s set has probability 1/3 (1 door), and the host’s set has probability 2/3 (2 doors).

When the host opens the door he is effectively altering the probabilities by adding the probability of the opened door to the sole remaining closed door [in his set], thereby increasing its probability to 2/3. In essence, the host just completed a filtering procedure to the benefit of the player, in plain sight.

At this stage, the player can choose to stay with his original choice or to switch doors. Given that the player’s choice remained unaffected throughout this procedure, it still has probability 1/3, whereas the other (now pre-selected) door has 2/3. Thus the winning strategy is to always switch.

Consider the following modified game. Assume there are one thousand closed doors, and the player picks one (not the winning choice). Then the host has a set of 999 doors to choose from and open—again, he can’t choose the winning choice—while leaving at least one door closed to present the dilemma. For the case when he goes and opens all but one door from his set (i.e. he opens 998/999 doors), then the player will have to choose between two doors: one with probability 1/1000 and the other with probability 999/1000. More generally for K doors, the probability of winning is 1/K for staying and (K-1)/K for switching.

Simulation

Law of Large Numbers

Code

def simulate(n_rounds=100):
    """
    Simulate Monty Hall games.

    Args:
        n_rounds: number of rounds to play
    Returns:
        staying_wins: list with n_round binary results, 1s are wins.
        switching_wins: list with n_round binary results, 1s are wins.
    """
    random.seed(99)
    door_set = {1, 2, 3}  # set of all doors
    staying_wins = []
    switching_wins = []
    for _ in range(n_rounds):
        prize_door = random.randint(1, 3)
        choice = random.randint(1, 3)  # player's choice
        # staying strategy:
        if choice == prize_door:
            staying_wins.append(1)
        else:
            staying_wins.append(0)
        # switching strategy:
        # the presenter may or may not have a choice:
            # if prize_door == players choice, 2 doors to choose from
            # else, there's only one door left
        host_choice = random.choice(list(door_set - {choice, prize_door}))
        new_choice = (door_set - {choice, host_choice}).pop()
        if new_choice == prize_door:
            switching_wins.append(1)
        else:
            switching_wins.append(0)
    return staying_wins, switching_wins