Deeplearning.ai 01: Neural Networks
Table of Contents
Summary
Notes for Andrew Ng’s Deep Learning Specialization Course 1.
Week 1
Representation of a Deep Neural Network:
Week 2
Image Representation
RGB channels: [Red, Green, Blue]
Example dimensions: 64x64x3. Unrolling RGB pixel intensity values results in a one-dimensional vector ∈ R (12288 x 1)
Notation:
- m_train = training examples
- m_test = test examples
Shapes for neural nets (NN):
\(
Y = [y^1, y^2, … , y^m] \quad Y ∈ R(1 \times m)
\)
\( X = [x^1, x^2, … , x^m] \quad X ∈ R(n \times m) \)
Y: a row vector. Each column contains the label for training example i
X: a matrix. Each column contains the feature vector for training example i
Linear Regression
\[ z = w^T.dot(x) + b\]
Where w is the vector of weights. There is one weight per feature. The prediction, ŷ, can be out of probability bounds [0, 1].
Vectors are conventionally initialized vertically. Therefore:
\( w^T \) is a row vector (ie horizontal)
\( x \) is a column vector (ie vertical)
\( w^T.dot(x) \) is a scalar and,
\( w^T.dot(x) + b \) is also a scalar
Logistic Regression (LR)
A probability is wanted:
$$ { ŷ = P(y=1 | x)} \quad ŷ \in [0,1] $$
The sigmoid function:
$$ \sigma(z) = \frac{1}{1+e^{-z}} = \frac{1}{1+ \frac{1}{e^z}} $$
if z is large: 1 / (1 + 0) ≈ 1
if z is small: 1 / (1 + BIG) ≈ 0
Activation function
$$ { \sigma(w^T.dot(X) + b) }$$
Goal: learn parameters W and b, so that ŷ^(i) is a good estimate for y^(i)
Note: superscript_i ^(i) refers to specific training-example_i
Next: in order to train a LR model, a loss/error function is needed
Example loss function
$$ { L(ŷ, y) = \frac{1}{2} (ŷ - y)^2 }$$
But, the squared error is not a good idea in logistic regression if it is to be trained with Gradient Descent (GD), because the optimization problem becomes non-convex, ie it has multiple local optima, GD may not ever converge on the global optimum. Instead, we can use (loss function for a single training example):
$$ { L(ŷ, y) = - ( ylogŷ + (1-y) log(1-ŷ) ) }$$
Intuition:
- if y = 1: L(ŷ, y) = -logŷ (we want ŷ large)
- if y = 0: L(ŷ, y) = -log(1-ŷ) (we want ŷ small)
The Cost Function extends the individual Loss Functions to the entire training set.
Generalization from Loss Function to Cost Function
To generalize the single-example Loss Function to a full training set with m examples, we do the following:
$$ { J(w, b) = (1/m) \sum_{i=1}^{m} L(ŷ^{(i)}, y^{(i)}) }$$
or, expanded out:
$$ { J(w, b) = -(1/m) \sum_{i=1}^{m} [ y^{(i)}logŷ^{(i)} + (1-y^{(i)}) log(1-ŷ^{(i)}) ] }$$
To train a Logistic Regression model, find parameters w, b (vectors, one element per feature) that minimize the Cost Function.
Gradient Descent
3Dimensions: [w, b, J(w,b)]
Goal: find values for w, b that minimize J(w, b)
Steps:
- Initialize w and b: for LR almost any initialization method works, usually (0,0) but random initialization also works.
- Take a step in the direction of the steepest descent
- Stop algorithm when no longer minimizing
Basic Derivative Review:
- slope == derivative == df(x)/x
- “height/width” or “rise/run” or \( \Delta y/ \Delta x \)
- x nudged from 2.0 to 2.001, y goes from 6.0 to 6.003;
- => derivative = 3
- Intuition dJ/dv: “if we were to take the value of v and change it a little, how would J change?"
Computation Graphs
- Forward Propagation: Compute the output (left to right)
- Backward Propagation: Compute derivatives (right to left)
Example function J(a,b,c):
u = bc; v = a + u; J = 3v
Chain rule:
dJ/da = dJ/dv * dv/da (a -> v -> J)
Convention for derivatives:
- d(FinalOutputVariable)/d(variable) == dvar
- Shortened to “dvar” (ie it is implied that the change of the intermediate variable “var” is assessed over the FinalOutputVariable)
Gradient Descent for Logistic Regression
Computation Graph:
[x1, w1, x2, w2, b] -> [Z = w1x1 + w2x2 + b] -> ŷ=a=sigmoid(Z) -> L(a,y)
Notation equivalence:
(L: loss function)
dw = dJ(w, b)/dw
db = dJ(w, b)/db
dZ = dL/dZ = dL(a,y)/dZ
da = dL/da = dL(a,y)/da
dw1 = dL/dw1
dw2 = dL/dw2
Derivative Calculus for LR:
(Y=ground truth vector doesn’t change, it makes no sense to compute dL/dy)
(X=feature vector, doesn’t change either)
da = -(y/a) + (1-y)/(1-a)
dZ = dL/da . da/dZ and,
da/dZ = a(1-a)
Therefore,
dZ = [-(y/a) + (1-y)/(1-a)] x a(1-a) = (a-y)
Then,
dw1 = x1dZ
dw2 = x2dZ
db = dZ
Gradient Descent on m examples

Once the entire loop is run (still one step), we can update the weights like so:
w1 := w1 - \(\alpha\)dw1
w2 := w2 - \(\alpha\)dw2
b := b - \(\alpha\)db
Vectorization – or the art of getting rid of explicit for loops in your code
Vectors are conventionally initialized vertically, therefore vec.T is horizontal
Computing usually slower by factor of 300x-400x using np.dot vs for loop
Parallelization instructions: Single instruction, multiple data (SIMD)
Vectorizing Logistic Regression
- row-vector: a one-dimensional vector that grows horizontally, ie entries are in cols
- col-vector: a one-dimensional vector that grows vertically, ie entries are in rows
X = [x^(1), x^(2), … , x^(m)] X ∈ R(n_x, m)(rows, cols)
ALERT: in traditional ML, x^(1), or the first column vector, is used to denote the feature vector containing values of feature x_1 for all training examples m. However, in deep learning, x^(1) denotes training example_1 across all its features. ie training examples grow horizontally and not vertically.
Prediction for training example 1
z^(1) = w^T.x^(1) + b
a^(1) = sigmoid(z^(1))
Predictions for 3 training examples
w^T.X + [b b b] (1,m) =
[w^T.x^(1)+b w^T.x^(2)+b w^T.x^(3)+b]
Z = [z^(1) z^(2) z^(3)] =
Z =
np.dot(w^T, X) + b
(1 x 1; b is a scalar but Python broadcasts it)
A = [a^(1) a^(2) a^(3)]
Vectorizing Gradient Descent
dz^(i) = a^(i) - y^(i)
dZ = [dz^(1) dz^(2) dz^(3)]
Y = [y^(1) … y^(m)]
dZ = A - Y = [a^(1)-y^(1) a^(2)-y^(2) …]
(…)
Full Vectorization for GD (all training examples, one iteration)
Z = w^T.X + b = np.dot(w^T, X) + b
A = sigmoid(Z)
J =
dZ = A - Y
dw = (1/m) X dZ^T
db = (1/m) np.sum(dZ)
Updates:
w := w - \(\alpha \)dw
b := b - \(\alpha \)db
Broadcasting (ie auto-expand)
- (axis=0) => across rows => vertically
- (axis=1) => across cols => horizontal
- (m,n) [+-*/] (1,n) ~> (m,n)
- (m,n) [+-*/] (m,1) ~> (m,n)
Week 3
Review Computation Graph for Logistic Regression
[x, w, b] -> z = w^T.X + b -> a = sigmoid(z) -> L(a, y)
New notation for Neural Nets (NN)
2-layer NN: [Input layer -> (1) Hidden layer -> Output layer]
layer: (usually) vertical stack of nodes
superscript_1 = [1] = quantities associated with layer_1
\( a_j^{[i]}\) = activation unit j in layer i
Example Computation for 2-layer NN and 1 training example
W^[1] -> z^[1] = W^[1].x + b^[1] -> a^[1] = σ(z^[1]) -> z^[2] = W^[2].a^[1] + b^[2] -> a^[2] = σ(z^[2]) -> L(a^[2], y)
What happens inside each activation unit (ie. node)
Two steps of computation:
- Step1: compute z = w^T.x + b
- Step2: compute \(\alpha(z)\) (ie activation)
Output Computation for Layer1_Node1 with 1 training example:
\({ z_1^{[1]} = w_1^{[1]T}.dot(x^{(i)}) + b_1^{[1]}}\)
\({ a_1^{[1]}=\alpha(z_1^{[1]}) }\)
NN Represetantion (1 training example)
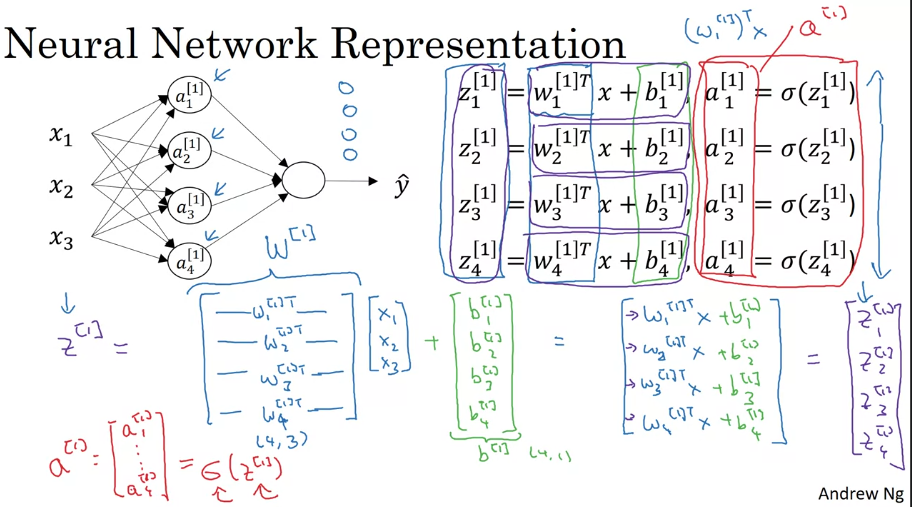
Associated parameters per layer:
$$ W^{layer}; b^{layer}; Z^{layer}; a^{layer} $$
Iterating through m examples (for loop version):
(Remember that each training example generates a prediction)
for i = 1 to m:
\( z^{[1][i]} = W^{[1]}.dot(x^{[i]}) + b^{[1]} \)
\( a^{[1][i]}=\alpha(z^{[1][i]}) \)
\( z^{[2][i]} = W^{[2]}.dot(a^{[1][i]}) + b^{[1]}\)
\( a^{[2][i]}=\alpha(z^{[2][i]}) \)
Extending to multiple training examples and vectorizing:

Activation matrix \( A^{[1]}\):
- \( A^{[1]}\).axis=0 (rows): iterates through hidden units in layer1
- \( A^{[1]}\).axis=1 (cols): iterates through training examples in layer1
Intuition: each hidden unit is “activated” iteratively by each training example
Activation functions
Activation functions are non-linear functions denoted by \(g(Z^{[i]})\), where i represents the layer. Different layers can use different activation functions. Some common activation functions are:
Why does a NN need a non-linear activation function?
(No activation function = identity activation function = linear activation function)
Because if only the identity activation function is used it doesn’t matter how many hidden layers the NN has, it will be equivalent to using a single linear function to make predictions;
ie. the composition of two linear functions is itself a linear function.
- Sigmoid:
- \( a = sigmoid(z) = 1/(1+e^{-z}) \)
- almost never used in practice. Exception: in the output layer under binary classification
- Hyperbolic tangent
- \( a = tanh(z) = e^{z} - e^{-z} / (e^{z} + e^{-z}) \)
- hyperbolic tangent is a shifted sigmoid, bounded \(-1 \leq y \leq 1\)
- useful because it centers the data around zero
- downside: if z is too large or small, the derivative will be close to 0, slowing down GD
- ReLU: Rectified Linear Unit
- \( a = max(0, z) \)
- derivative is 1 so long as z is positive
- derivative of 0.000 is not defined, but it’s also unlikely in practice to reach that number because of decimals
- Leaky ReLU:
- \( a = max(0.01z, z) \)
- fixes negative derivatives when z is negative
Rules of thumb for Activation function selection:
- difficult to know in advance, depends on the problem, test multipe choices
- for hidden layers, use ReLu
- for the output layer (if binary classification), use sigmoid(z)
- if doing ML on a regression problem like predicting housing prices (y is a real number), it’s advisable to actually use a linear function for the output layer (only, keep non-linear activation functions for the hidden layers)
Derivatives of activation functions
convention: \( dg(z)/dz = g'(z) \)
- Sigmoid
\( g'(z)= g(z) (1-g(z)) = a(1-a) \) - Tanh
\( g'(z)= g(z) (1-g(z))^2 = 1-a^2 \) - ReLU
$$ g'(z)= \begin{cases} 0 & \text{if } z<0 \cr 1 & \text{if } z>0 \cr undefined & \text{if } z=0 \end{cases} $$
- Leaky ReLU
$$ g'(z)= \begin{cases} 0.01 & \text{if } z<0 \cr 1 & \text{if } z>0 \cr undefined & \text{if } z=0 \end{cases} $$
Gradient Descent for NN

Random Initialization
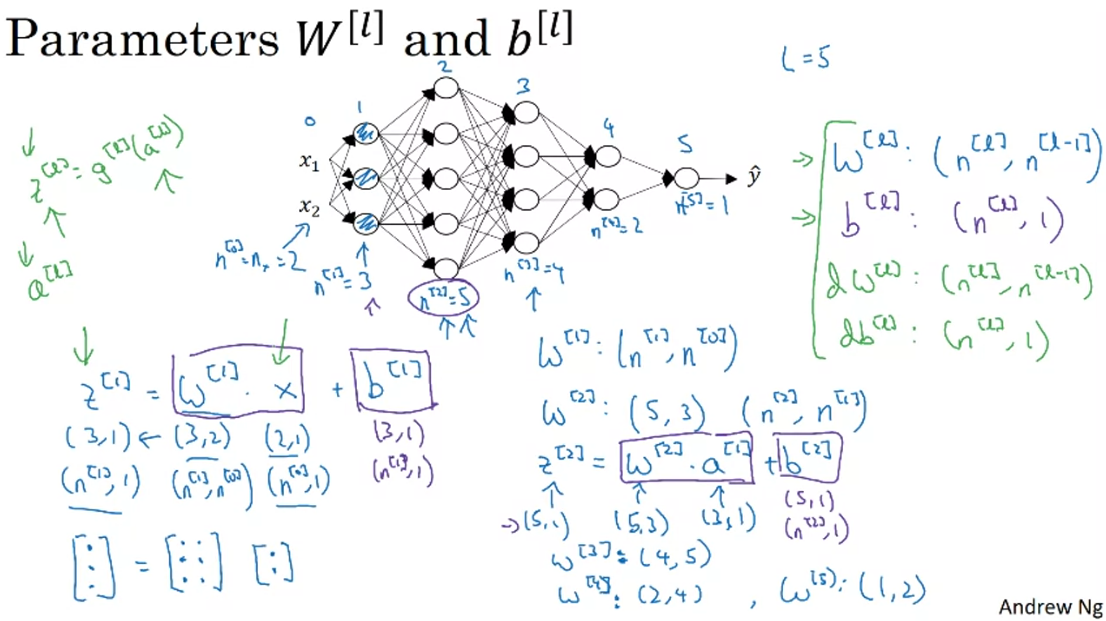
Remember, \( W^{[1]} \) is the matrix of weights for layer 1, with dimensions:
- Rows: number of activation units (ie nodes) in layer 1
- Columns: number of input units (ie features for L1)
If weights are initialized to zero in a NN, then for any given example in the training set, \( a_1^{[1]} = a_2^{[1]} \). Hidden units like these have identical outputs and are called “symmetrical”. Then, for every step of Gradient Descent, every row of the dW matrix will be identical also.
In general, initializing all the weights to zero results in the network failing to break symmetry. This means that every neuron in each layer will learn the same thing, and you might as well be training a neural network with \( n^{[l]}=1 \) for every layer, and the network is no more powerful than a linear classifier such as logistic regression. Therefore, the goal is to have different activation functions in each hidden unit.
Note: initializing b^[1] to zero is not a problem.
Recommended approach:
W^[1] =
np.random.randn((2,2)) * 0.01
b^[1] =np.zero((2,1))
The intuition behind the 0.01 constant multiplication in the initialization stage is to avoid large numbers in the calculation for \(Z\). Large numbers move the value in the activatuion function towards the tails, which in turn makes the derivative fairly small, thus slowing down Gradient Descent, we want to avoid this.
Week 4
Deep Neural Net Notation
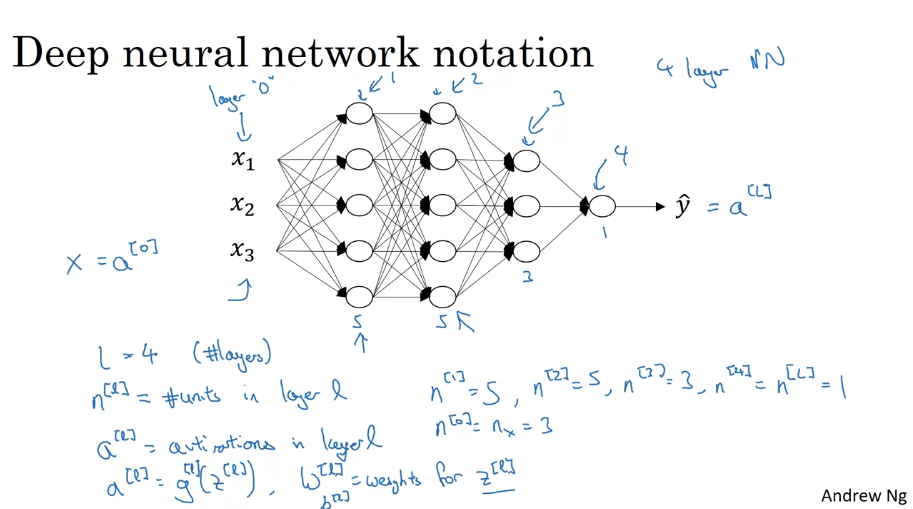
Dimensions for a single example
Forward and Backward Prop
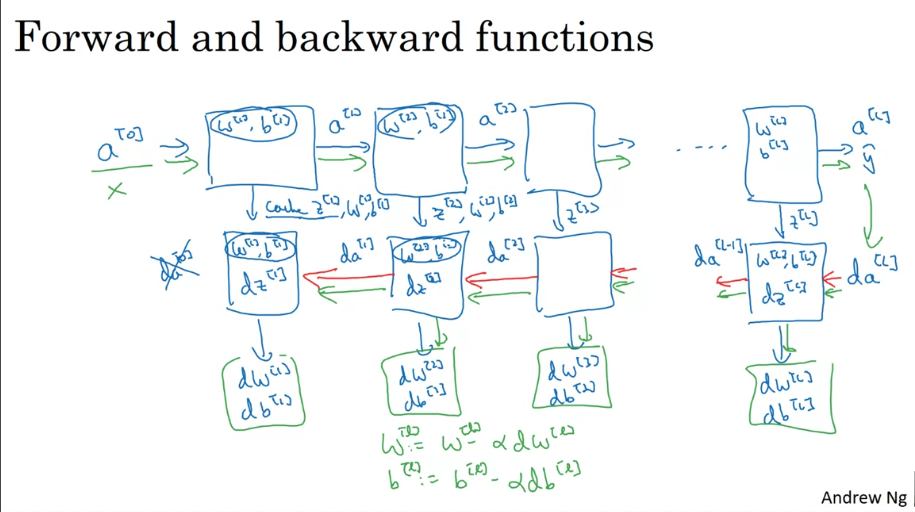
Forward Propagation
Vectorized version:
\( Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]} \) (1)
\( A^{[l]}=g^{[l]}(Z^{[l]}) \) (2)
Note: the final activation function is the final output (ie prediction)
Note2: there is an unavoidable for loop to iterate through the layers
Backward Propagation
Deep NN Representation Depth
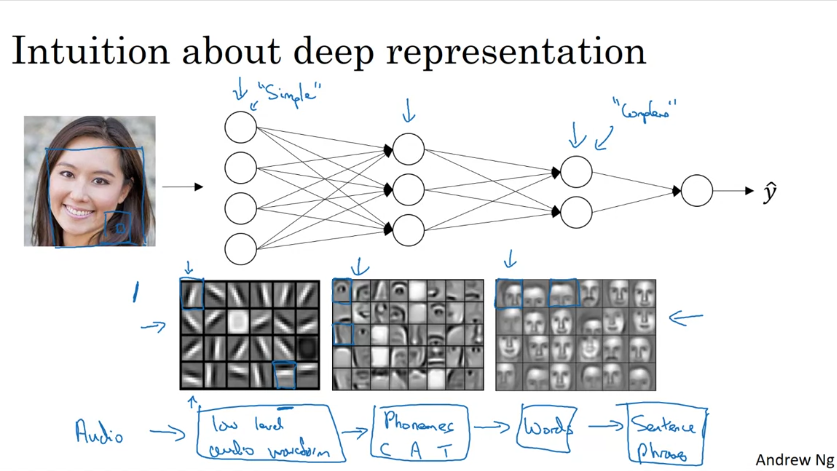
Parameters and Hyperparameters
Parameters:
- \( W^{[l]}, b^{[l]} \)
Hyperparameters (ie parameters that control the pamaeters):
- Learning rate \( \alpha \)
- Iterations of Gradient Descent
- Hidden Layers L
- Hidden Units \( n^{[1]}, n^{[2]}, … \)
- Choice of activation function
- etc